Merkezcil Kuvvet ve Merkezkaç Kuvveti Nedir?

Çoğu insan merkezcil ve merkezkaç kuvvetini duymuştur. Hangisinin ne olduğunu takip etmek biraz zor olsa da, bu iki kavramı duyan herkes, birinin dönme sırasındaki nesnelerin içe doğru hareket etme eğilimi olduğunu ve diğerinin ise dönen nesnelerin dışa doğru hareket etme eğilimi olduğunu hatırlar.

O halde, tam anlamıyla merkezkaç (dışa doğru) kuvvet gibi bir şeyin olmadığını öğrenmek şaşırtıcı olabilir. Yalnızca merkezcil (içe doğru) kuvvet ve belirli durumlarda dönmekte olan nesnelerin dışa doğru hareket etmesini sağlayan eylemsizlik vardır, örneğin, dönüş yapan bir araba, bir hız treninin hareketi - hatta bir santrifüjün dönmesi.

Nasıl Çalışır?

Fizikteki diğer birçok ilke gibi, merkezcil kuvvet de nihayetinde hareketin temelleri ile ilgili birkaç basit ilkeyle ilgilidir. Düzgün dairesel harekette olan bir nesneyi düşünün: nesne bir dairenin merkezi etrafında hareket eder, böylece hızı sabit veya değişmez. Hızın formülü - veya daha doğrusu ortalama hız - mesafenin zamana bölünmesidir; bu nedenle insanlar örneğin "mil (veya kilometre) / saat" derler.

Daire oluşturan bir nesne durumunda, mesafe dairenin çevresine veya etrafındaki mesafeye eşittir. Geometriden, bir çemberin çevresini hesaplamak için formülün 2 πr olduğunu biliyoruz, burada r yarıçap veya çevreden merkeze olan uzaklıktır. Şekil Π, 3.141592 olarak gösterilebilir… aslında irrasyonel bir sayıdır: ondalık rakamlar sonsuza kadar tekrarlama veya desen olmadan devam eder.

Yukarıdakilerden, bir daire etrafında hareket eden bir nesnenin ortalama hızının formülünün 2 πr bölü zaman olduğu anlaşılabilir. Ayrıca, yarıçap ile ortalama hız arasında orantılı bir ilişki olduğunu görebiliriz.

Bir dairenin yarıçapı iki katına çıkarsa, ancak dairenin çevresindeki bir nesne daha önce olduğu gibi aynı miktarda tam bir dönüş yaparsa, bu ortalama hızın da iki katına çıktığı anlamına gelir. Bu, biri 2 yarıçaplı, diğeri 4 yarıçaplı iki daire oluşturarak ve rastgele bir zaman aralığı (örneğin 2 saniye) kullanarak gösterilebilir.

Yukarıdaki sonuç, bir dairenin yarıçapı boyunca farklı noktalardaki hızlarla ilgili ilginç bir çıkarım taşıyor. Aynı zaman diliminde iki farklı dairenin çevresi etrafında hareket eden iki noktayı (biri diğerinin iki katı kadar büyük) karşılaştırmak yerine, bu iki nokta aynı daire üzerinde olabilir: biri çevrede ve diğeri yarıçapın tam ortasında.

Her ikisinin de aynı süre içinde tam bir daire seyahat ettiğini varsayarsak, daha önce açıklanan orantılı ilişki geçerli olacaktır. Bu, o zaman, daire üzerinde ne kadar dışarı çıkılırsa, ortalama hız o kadar büyük olur.

Hız = Sürat + Yön

Sürat skalerdir, yani büyüklüğü vardır ancak belirli bir yönü yoktur; tersine, hız bir vektördür - hem büyüklüğü (yani hızı) hem de yönü olan bir niceliktir. Dairesel hareket halindeki bir nesne için, hızının yönü, nesnenin herhangi bir noktada hareket ettiği yön ile aynıdır.

Atlanta, Georgia ve Interstate-285 kentini, bir şehrin bir "döngü" karayolu ile çevrili olduğu birkaç örnekten birini düşünün. Yerel trafik muhabirleri, o karayolu üzerindeki noktalar için sadece yön koordinatları vermekten kaçınır (örneğin, "285'te güneye doğru"), çünkü trafiğin güneye doğru hareket ettiği alan, birinin saat yönünde mi yoksa saat yönünün tersine mi hareket ettiğine bağlıdır. Bu nedenle, muhabirler genellikle "dış döngüde güneye doğru" derler.

I-285'teki arabalarda olduğu gibi, bir daire etrafında hareket eden bir nesne için hız vektörünün yönü, dairenin kendisi için tamamen konumunun ve hareket yönünün (saat yönünde veya saat yönünün tersine) bir işlevidir. Herhangi bir noktadaki bireysel hız vektörünün yönü teğetsel olarak tanımlanabilir; yani, bir tanjantı veya daireye sadece bir noktada dokunan bir çizgiyi tanımlıyor. (Tanım gereği teğet doğru çemberle kesişemez.)

O halde, bir daire etrafında hareket halindeki bir nesnenin yönü değişiyor; dolayısıyla hızı da değişiyor ve bu da ivme yaşadığı anlamına geliyor. Merkezcil kuvvet ve "merkezkaç kuvveti" konusunda olduğu gibi, çoğu insan hızlanmanın sadece süratte bir artışa atıfta bulunduğuna inanarak yanlış bir ivme görüşüne sahiptir.

Aslında ivme, hızdaki bir değişikliktir ve bu nedenle sürat veya yöndeki bir değişikliği ifade edebilir. Bu değişimin olumlu olması da gerekli değildir; başka bir deyişle, süratte düşüş yaşayan bir nesne de hızlanma yaşar.

Dönme hareketindeki bir nesnenin ivmesi her zaman dairenin merkezine doğrudur. Bu, ivmenin hız ile aynı yönde hareket ettiğini göstermesi gereken sağduyuya aykırı gibi görünebilir, ancak aslında birkaç yolla kanıtlanabilir.

Bir yöntem vektörlerin eklenmesi olabilir, ancak "uygulamalı" bir gösteri, soyut bir geometrik kanıttan daha aydınlatıcı olabilir. Bir camın içinde yanan bir mum ile basit bir ivmeölçer, ivmeyi ölçmek için bir cihaz yapmak mümkündür.

Kütle × İvme = Kuvvet

Bir daire etrafında dönen bir cisim için ivmenin var olduğunu gösterdiğimizden, cismin bir tür kuvvetle karşılaştığını kanıtlamamız mümkündür. Bu iddianın kanıtı, kuvveti kütlenin ve ivmenin ürünü olarak tanımlayan ikinci hareket yasasında yatmaktadır: bu nedenle, ivme ve kütlenin olduğu yerde kuvvet olmalıdır. Kuvvet her zaman ivme yönündedir ve bu nedenle kuvvet dairenin merkezine doğru yönlendirilir.

Yukarıdaki paragrafta, kütlenin varlığını varsaydık, çünkü tartışma boyunca bir daire etrafında dönen bir nesne ile ilgiliydi. Tanımı gereği bir nesne - yani hayali bir noktadan ziyade maddenin bir öğesi - bir kütleye sahiptir. Kütle, birinci hareket yasası ile açıklanabilecek bir eylemsizlik ölçüsüdür: hareket halindeki bir nesne, üzerine bir dış kuvvet etki etmedikçe veya etki edene kadar aynı hızda ve aynı yönde hareket halinde kalma eğilimindedir. Başka bir deyişle, hareketsiz duran bir nesnenin hareketsiz kalmasına neden olan eylemsizliktir ve aynı şekilde, hareket eden bir nesnenin hareket etmeye "çalışacağını" belirleyen de eylemsizliktir.

Merkezcil Kuvvet

Şimdi dönme hareketinde bir kuvvetin varlığını belirlediğimize göre, ona bir isim vermek mümkündür: merkezcil kuvvet veya düzgün dairesel hareket halinde bir nesnenin dairesel yolun merkezine doğru hareket etmesine neden olan kuvvet.

Bu "yeni" bir güç türü değildir; sadece dairesel veya dönme hareketinde uygulanan kuvvettir ve kesinlikle gereklidir. Bu nedenle, fizikçiler bir "merkezcil kuvvet gerekliliğinden" bahseder: merkezcil kuvvetin yokluğunda, bir nesne basitçe dönemez. Bunun yerine, düz bir çizgide hareket edecektir.

Merkezcil Latince "merkezi aramak" anlamına gelir." Öyleyse, "merkezden kaçmak" anlamına gelen merkezkaç nedir? Merkezkaç hareketi diye bir şey var demek doğru olur; ancak merkezkaç kuvveti oldukça farklı bir konudur. Merkezcil kuvvet ile sadece merkezkaç eğilimi arasındaki fark - kuvvetten ziyade eylemsizliğin bir sonucu - tanıdık bir örneğe atıfta bulunularak açıklanabilir.

Gerçek Hayattan Uygulamalar

Araba Sürmek

Bir arabaya bindiğinizde ve araba hızlandığında, vücudunuz koltuğa karşı geriye doğru hareket etme eğilimindedir. Aynı şekilde, araba aniden durursa, vücudunuz gösterge paneli yönünde ileri doğru hareket etme eğilimindedir. Buradaki dile dikkat edin: "itme" yerine "hareket etme eğilimindedir".

Bir şeyin itildiğini söylemek, bir kuvvetin uygulandığını gösterir, ancak burada iş başında olan şey bir kuvvet değil, eylemsizliktir - hareket halindeki bir nesnenin hareket halinde kalma eğilimi ve hareketsiz bir nesnenin hareketsiz kalma eğilimi.

Hareket etmeyen bir araba, tanımı gereği hareketsizdir ve sürücü de öyle. Araba hareket etmeye başladığında, böylece hızda bir değişiklik yaşandığında, sürücünün vücudu hala sabit konumda kalma eğilimindedir.

Dolayısıyla, sürücüyü koltuğa doğru geriye iten bir kuvvet değildir; daha ziyade, kuvvet otomobili ileri itti ve koltuk, sürücünün sırtını karşılamak için yukarı hareket etti. Dururken, bir kez daha, hızda belirli bir değerden sıfıra ani bir değişiklik olur. Bu arada sürücü, eylemsizlik nedeniyle ilerlemeye devam ediyor ve bu nedenle, vücudunun artık hareketsiz gösterge paneli yönünde hareket etmeye devam etme eğilimi var.

Bu, eylemsizlik üzerine çalışan herkes için biraz fazla basit görünebilir, ancak insan zihninin eylemsizliği kendi içinde bir güç olarak algılamaya çok eğilimli olması nedeniyle, en temel terimlerle açıklığa kavuşturulması gerekir.

Bu alışkanlık, yan taraftaki başka bir araç geriye doğru hareket ederken, hareketsiz duran bir araçta otururken yaşadığınız deneyime benzer. Farkındalığın ilk iki saniyesinde, zihniniz diğer arabanın geriye doğru hareketini oturduğunuz arabanın ileri doğru hareket olarak yorumlama eğilimindedir - kendi arabanız hareketsiz dursa bile.

Şimdi merkezcil kuvvetin etkilerini ve merkezkaç kuvvetinin yanılsamasını ele alacağız. Bir araba sola döndüğünde, 90 ° 'lik bir açıyı veya bir dairenin dörtte birini tanımlayan bir rotasyon şekline giriyor. Dönüşün başında araba ile birlikte hareket halinde olduğu için vücudunuz bir kez daha eylemsizlik yaşar ve böylece ileriye doğru hareket etme eğilimindesiniz.

Araba aynı zamanda kendi eylemsizliğini büyük ölçüde aşmış ve sola dönüşe geçmiştir. Böylece arabanın kapısının kendisi sola doğru hareket ediyor. Kapı vücudunuzun sağ tarafıyla buluştuğunda, kapıya karşı dışa doğru itilme hissi yaşarsınız, ama aslında olan şey kapının içe doğru hareket etmesidir.

Merkezkaç kuvveti yanılsaması, halkın hayal gücüne o kadar derinden yerleşmiştir ki, aşağıda daha fazla tartışmayı gerektirmektedir. Ancak bir otomobile binme konusunda, merkezcil kuvvetin başka bir örneğini incelememiz gerekir.

Bu bağlamda, bir arabanın dönüş yapması için, lastikler ile yol arasında sürtünme olması gerektiğine dikkat edilmelidir. Sürtünme, bir nesnenin yüzeyi diğerinin yüzeyiyle temas ettiğinde harekete direnen kuvvettir; yine de ironik bir şekilde, harekete karşı çıkarken, sürtünme de göreceli hareketi mümkün kılar.

Öyleyse, bir sürücünün dönüş yaparken fren yaptığını varsayalım. Bu şimdi merkezcil kuvvete teğetsel veya dik açıda bir kuvvet ekler. Bu kuvvet merkezcil kuvvetten daha büyükse, yani araç çok hızlı hareket ediyorsa, araç dönüş yapmak yerine ileri kayacaktır. Bu durumda olan herkesin onaylayacağı gibi sonuçlar felaket olabilir.

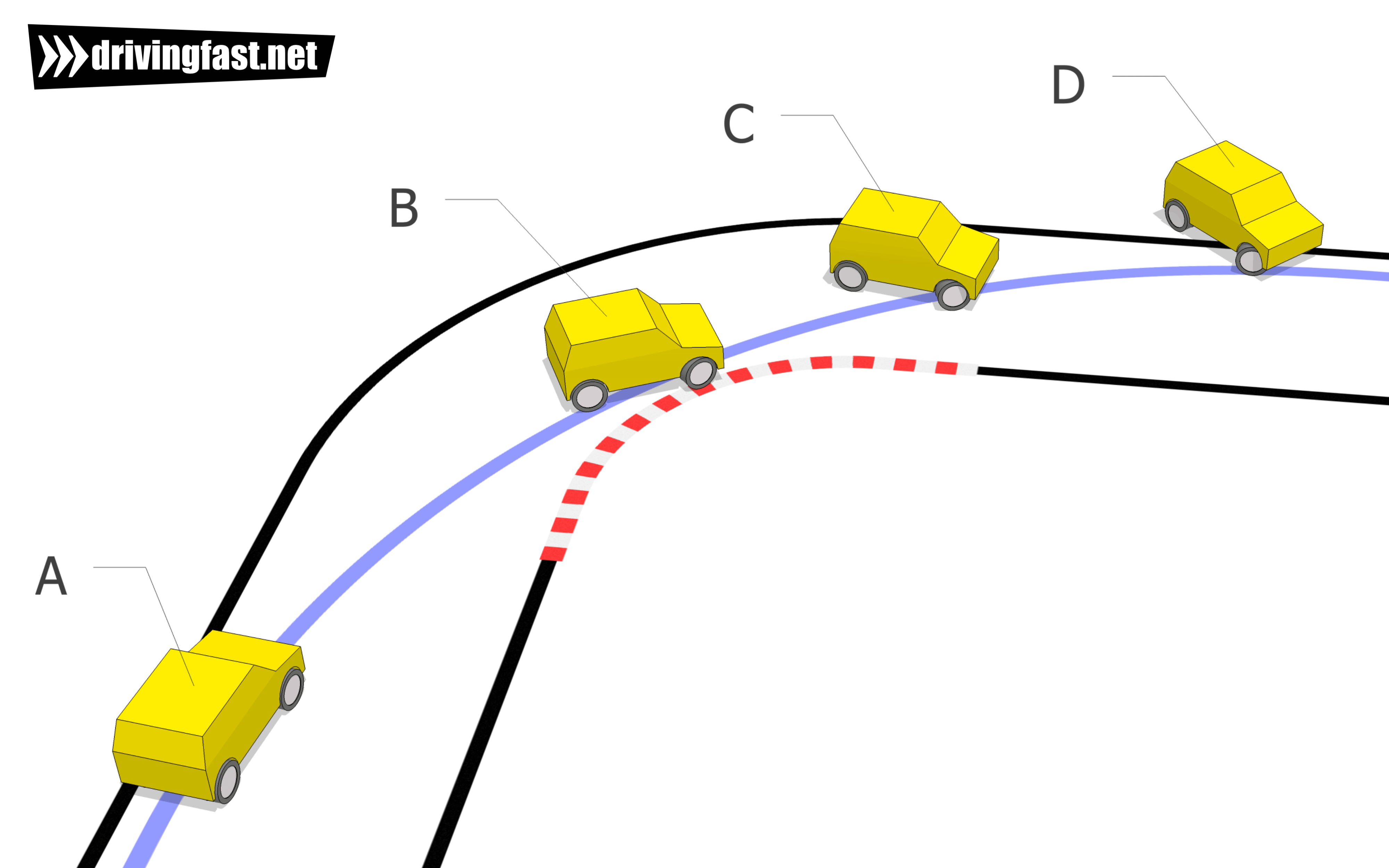
Yukarıdakiler merkezcil kuvvet gerekliliğinin önemini vurgulamaktadır: Yeterli derecede merkezcil kuvvet olmadan, bir cisim dönemez. Eğriler genellikle merkezcil kuvveti en üst düzeye çıkarmak için kümelenmiştir, bu da yolun viraj yönünde içe doğru eğildiği anlamına gelir. Bu viraj, hızda ve dolayısıyla ivmede bir değişikliğe neden olarak, araca dönüşü yapmak için gerekli merkezcil kuvveti sağlayan, reaksiyon kuvveti olarak bilinen ek bir miktarla sonuçlanır.

Bir eğrinin yatması gereken açıyı hesaplama formülü, aracın hızını ve viraj açısını hesaba katar, ancak aracın kütlesini içermez. Sonuç olarak, karayolu departmanları, araçların dönüşü hangi hızda yapması gerektiğini belirten işaretler asarlar, ancak bu işaretlerin verilen modellerin ağırlığına ilişkin özel ifadeler içermesi gerekmez.

Santrifüj

Daha önce belirtildiği gibi gerçekten sadece merkezkaç hareketi olan "merkezkaç kuvveti" konusuna geri dönmek için, "Merkezkaç kuvveti diye bir şey yoksa, santrifüj nasıl çalışır?" Diye sorabilirsiniz. Tıpta ve çeşitli bilimlerde yaygın olarak kullanılan bir santrifüj, bir sıvı içindeki parçacıkları ayıran bir cihazdır. Örneğin bir uygulama, kırmızı kan hücrelerini plazmadan ayırmaktır.

Tipik olarak bir santrifüj bir tabandan oluşur; tabana dik dönen bir tüp; ve hareketli santrifüj kolları ile dönen tüpe tutturulmuş iki şişe. Hareketli kollar, dönen borunun tepesinde menteşelidir ve bu nedenle, boruya 90 ° yaklaşan bir açıyla yukarı doğru hareket edebilir. Tüp dönmeye başladığında merkezcil kuvvet, şişelerdeki malzemeyi merkeze doğru çeker.

Daha yoğun olan malzemeler daha büyük eylemsizliğe sahiptir ve bu nedenle merkezcil kuvvete daha az duyarlıdır. Bu nedenle, dışarı doğru itilmiş gibi görünüyorlar, ancak gerçekte olan, daha az yoğun olan malzemenin içe doğru çekilmesidir.

Bu, örneğin üstte plazma ve altta kırmızı kan hücreleri olmak üzere bileşenlerin ayrılmasına yol açar. Yine, plazma o kadar yoğun değildir ve bu nedenle daha kolay dönme merkezine doğru çekilirken, kırmızı kan hücreleri daha az tepki verir ve sonuç olarak altta kalır.

Santrifüj

Santrifüj, 1883'te, kremayı sütten ayırmak için kullanan İsveçli bir mühendis olan Carl de Laval (1845-1913) tarafından icat edildi. 1920'lerde, İsveçli kimyager Theodor Svedberg (1884-1971), benzer ağırlıktaki çok küçük parçacıkları ayırmak için kullanılan ultra santrifüjü yaratmak için Laval'ın çalışmalarını geliştirdi.

Tipik bir ultrasantrifüjde, flakonların çapı 0,2 inç'ten (0,6 cm) büyük değildir ve bunlar dakikada 230.000 devire kadar hızlarda dönebilir. Endüstride kullanılan santrifüjlerin çoğu dakikada 1.000 ila 15.000 devir arasında bir aralıkta döner, ancak bilimsel uygulamaları olan diğerleri çok daha yüksek bir hızda döner ve yerçekimininkinden 25.000 kat daha büyük bir kuvvet üretebilir.

1994'te, Colorado Üniversitesi'ndeki araştırmacılar, barajlara ve diğer büyük yapılara uygulanan gerilmeleri simüle etmek için bir tür süper santrifüj yarattılar. Cihaz, test edilecek yapının ölçek modelini içeren bir sallanan sepetin bağlı olduğu 19.69 ft (6 m) ölçülerinde sadece bir santrifüj koluna sahiptir. Model, gerçek yapının 1 / 50'si boyutundaysa, santrifüj, yerçekiminin 50 katı bir merkezcil kuvvet oluşturacak şekilde ayarlanır.

Colorado santrifüjü, patlamaların binalar üzerindeki etkilerini test etmek için de kullanıldı. Merkezcil, yerçekimi ve patlamanın kendisininki gibi kuvvetlerin birleşimi çok büyük olduğu için, bir binanın modeli üzerindeki patlamanın etkilerini ölçmek için çok az miktarda patlayıcı gerekir.

Eve daha yakın, sıkma döngüsündeki bir çamaşır makinesi Bir tür santrifüjdür. Islak giysiler döndükçe, içlerindeki su, giysilerin kendisinden ayrılarak dışarıya doğru hareket etme eğilimindedir. Bir ipe oldukça ağır bir ağırlık bağlayarak ve onu başının üzerine sallayarak daha da basit, daha aşağıya doğru bir santrifüj oluşturulabilir: Bir kez daha, ağırlık dışarıya doğru itilmiş gibi davranır, ancak gerçekte sadece eylemsizliğe yanıt verir.

Hız Trenleri ve Merkezcil Kuvvet

İnsanlar, deneyimledikleri heyecan için elbette lunapark trenine binerler, ancak bu heyecanın hızdan çok merkezcil kuvvetle ilgisi vardır. Yirminci yüzyılın sonlarında, 90 mil / saatin (144 km / s) üzerinde hız yapabilen lunapark trenleri Amerika'daki eğlence parklarında görünmeye başladı; ancak o zamandan önce, bir lunapark treninin gerçek hızları pek etkileyici değildi.

Nadiren, otoyolda ilerleyen bir arabanınkini aştılar. Öte yandan, bir hız treni üzerinde üretilen hızlanma ve merkezcil kuvvet yüksektir ve gerçekten akılda kalan bir ağırlıksızlık (ve bazen ağırlıksızlığın tersi) duygusu taşır.

Parkurun geri kalanı genellikle eğimler ve tepeler, yatık dönüşler ve bazı durumlarda koton halkalardan oluşur. İkincisi, baş aşağı bir gözyaşı damlası gibi, bezoid olarak bilinen geometrik bir şekle işaret eder. Bezoidin şekli nedeniyle, üstte alt kısma göre çok daha küçük bir yarıçapı vardır - bu döngülerden hız treni sürüşünün çalışmasında önemli bir faktördür.

Geçmiş günlerde, hız treni tasarımcıları, arabaların çok yüksek hızlarda girmesine izin veren, çok fazla kuvvet oluşturan ve biniciler için yaralanmalara neden olan mükemmel dairesel döngüler kullandılar. Sonunda mühendisler, Euler spiraliyi güvenli ve eğlenceli bir sürüş sağlamanın bir yolu olarak gördüler.

Euler spirali (eğimi eğrinin uzunluğuyla doğrusal olarak değişen bir eğridir. Euler spiralleri yaygın olarak spiros, clothoids veya Cornu spiralleri olarak da adlandırılır.) halkaya girerken, sonra yukarı, sonra tekrar ve aşağı hareket ederken, sürekli olarak konum değiştirirsiniz. Döngüden yukarı çıkarken, hız treni kinetik enerjideki veya bir nesnenin hareketi nedeniyle sahip olduğu enerjideki bir düşüş nedeniyle yavaşlar.

Döngünün tepesinde, hız treni büyük miktarda potansiyel enerji kazanmıştır veya bir nesnenin konumu nedeniyle sahip olduğu enerji ve kinetik enerjisi sıfırdadır. Fakat diğer taraftan aşağı inmeye başladığında, kinetik enerji - ve onunla birlikte hızı - bir kez daha hızla artar.

Kinetik ve potansiyel enerji gibi - inişler ve tepelerle uygun şekilde yükselip alçalan - normal kuvvet ve yerçekimi kuvveti, hız treni sürüşü boyunca bir tür "rekabet" içinde kilitlenir. Hız treninin doğru etkiye sahip olması için, normal kuvvetin çoğu yerde yerçekimini aşması gerekir.

Bir hız treni sürüşü üzerindeki normal kuvvetteki artış, yerçekiminden başka bir şey deneyimlemenize neden olan ivme ve merkezcil harekete bağlanabilir. Bu nedenle, bir döngünün tepesinde normalden daha hafif ve altta daha ağır hissedersiniz. Aslında, kilonuzda gerçek bir değişiklik olmadı: bu, daha önce tartışılan "merkezkaç kuvveti" fikri gibi, bir algı meselesidir.

Anahtar Terimler

Merkezkaç: Düzgün dairesel hareket halindeki nesnelerin dairesel yolun merkezinden uzaklaşma eğilimini tanımlayan bir terim. "Merkezkaç kuvveti" terimi sıklıkla kullanılsa da, nesnenin dışarı doğru hareket etmesine neden olan şey kuvvetten ziyade eylemsizliktir.

Merkezcil Kuvvet: Düzgün dairesel hareketteki bir nesnenin dairesel yolun merkezine doğru hareket etmesine neden olan kuvvet.

Eylemsizlik: Hareket halindeki bir nesnenin hareket halinde kalma ve hareketsiz bir nesnenin hareketsiz kalma eğilimi.

Kaynak

Aylesworth, Thomas G. Science at the Ball Game. New York: Walker, 1977.

Beiser, Arthur. Fizik, 5. Baskı. Okuma, MA: Addison-Wesley, 1991.

Buller, Laura ve Ron Taylor. Doğanın güçleri. John Hutchinson ve Stan North tarafından çizimler. New York: Marshall Cavendish, 1990.

"Santrifüj Kuvveti - Dönme Hareketi." Ulusal Havacılık ve Uzay Dairesi (Web sitesi). <http://observe.ivv.nasa.gov/nasa/space/centrifugal/centrifugal3.html> (5 Mart 2001).

"Dairesel ve Uydu Hareketi" (Web sitesi). <http://www.glenbrook.k12.il.us/gbssci/phys/Class/circles/circtoc.html> (5 Mart 2001).

Cobb, Vicki. Dünya Neden Düşmüyor? Ve Hareket Hakkında Bu Kadar Saçma Olmayan Diğer Sorular. Ted Enik tarafından çizilmiştir. New York: Lodestar Kitapları, 1988.

Lefkowitz, RJ Push! Çek! Dur! Git! Kuvvetler ve Hareket Hakkında Bir Kitap. June Goldsborough tarafından çizilmiştir. New York: Parents 'Magazine Press, 1975.

"Dönme Hareketi." Physics Department, University of Guelph (Web sitesi). <http://www.physics.uoguelph.ca/tutorials/torque/> (4 Mart 2001).

Schaefer, Lola M. Dairesel Hareket. Mankato, MN: Pebble Books, 2000.

Snedden, Robert. Kuvvetler. Des Plaines, IL: Heinemann Kütüphanesi, 1999.

Whyman, Kathryn. Eylemdeki Kuvvetler. New York: Gloucester Press, 1986.